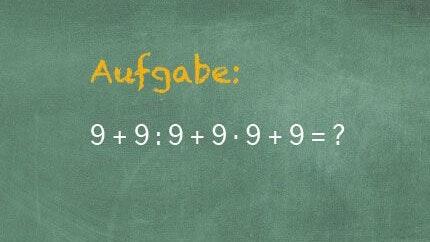
In der Schulzeit waren wohl viele einfach nur froh, wenn sie die Matheklausuren bestanden und mit der Mathematik nach dem Abschlusszeugnis nichts mehr zu tun hatten. Doch ganz so einfach kommt man eben doch nicht um das nicht ganz so beliebte Schulfach herum. Denn schließlich lauern auch im Alltag jede Menge Zahlen und Rechnungen. Und da passieren leicht mal Fehler.

Einer, der solche Fehler und falsche Rechnungen kennt, ist Hans Stefan Siller, Mathematik-Professor an der Universität Würzburg. Anlässlich des "I Love Mathe"-Tages an diesem Sonntag, 12. November, zeigt er sechs einfache Rechenwege, die immer wieder gern falsch gemacht werden. Und wie es besser gehen kann.
1. Fehler: Bei Proportionsrechnungen automatisch immer die Faustregel anwenden

Die Proportionsrechnung ist für viele Menschen tückisch, denn viele würden nach der Faustregel "je mehr, desto mehr" vorgehen, sagt Hans Stefan Siller. Häufig sei das zwar richtig, aber eben nicht immer. "'Je mehr ich kaufe, desto mehr muss ich bezahlen' – in diesem Kontext mag die Annahme stimmen", sagt der Mathe-Prof
In anderen Situationen aber nicht. Zum Beispiel beim Kochen. Wenn man ein Ei 7,5 Minuten in heißem Wasser kochen muss, damit es hart wird, dann muss man bei 5 Eiern im Topf das Wasser
eben nicht 37,5 Minuten kochen. Sondern immer noch nur 7,5 Minuten. "Da sollte man dann den Hausverstand einschalten, wie wir in Österreich sagen würden", sagt Siller.
2. Fehler: Punkt-vor-Strichrechnung nicht beachten
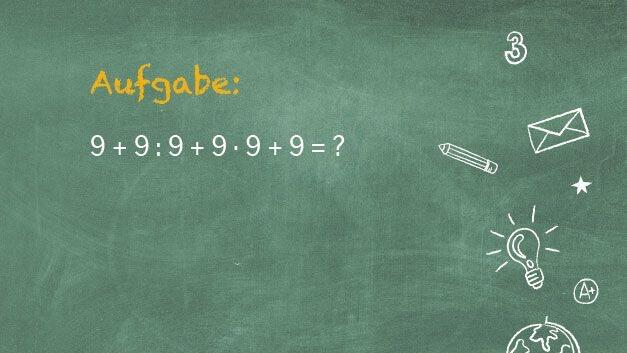
Auch wenn seinen Studierenden das nicht mehr passiert, zählt das Missachten der Regel "Punkt-vor-Strichrechnung" wohl mit zu den häufigsten mathematischen Fehlern, sagt der Mathe-Professor. Oft versuche man, Aufgaben einfach drauflos auszurechnen, ohne sich dabei an das in der Schule Gelernte zu erinnern.
Dabei kann es eigentlich so einfach sein:

3. Fehler: Binomische Formel nicht anwenden, sondern einfach quadrieren

Hier begehen vor allem viele Schülerinnen und Schüler einen klassischen Fehler, weiß Siller. "Da wird häufig einfach alles in der Klammer quadriert." Das ist jedoch falsch, denn was hinter der Aufgabe steht, ist eigentlich die Flächeninhaltsformel eines Quadrates.
Und eben diese löst man nicht durch einfaches Quadrieren, sondern durch das Anwenden der binomischen Formel:
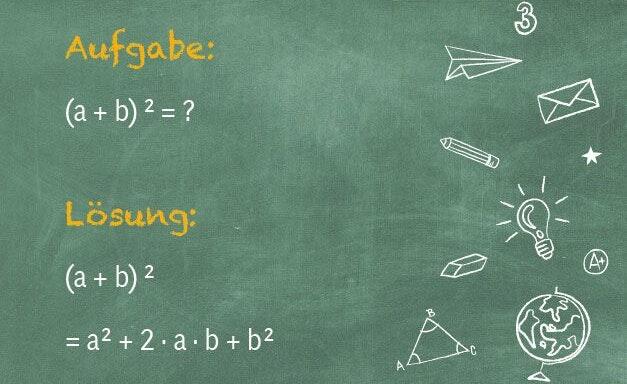
4. Fehler: Brüche einfach zusammenrechnen, weil ein Plus dazwischen steht
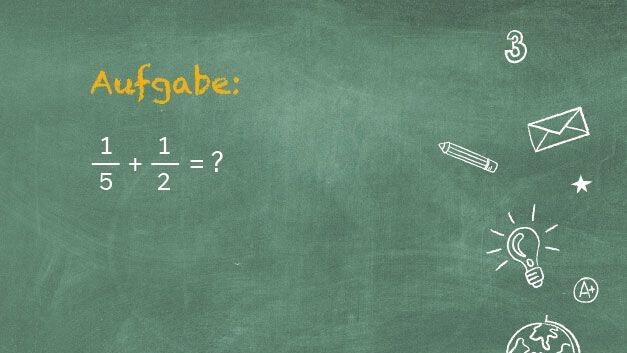
Auch solche Fehler sehe Siller immer wieder. Statt den Bruch auf einen gemeinsamen Nenner zu bringen, würden viele nur auf das Pluszeichen achten und beide Brüche einfach zusammenrechnen. Doch so funktioniert Bruchrechnung nicht.
Silers Tipp, damit solche Fehler in Zukunft nicht mehr passieren: Er schlägt vor, sich bei den Brüchen einfach an Getränken zu orientieren. "Wenn Sie ein Viertel Wein trinken und dann noch ein Viertel Liter Wein trinken, dann haben Sie einen halben Liter Wein getrunken." Und eben nicht nur ein Achtel. Das sei für viele einleuchtend und eine kleine Eselsbrücke.
Und so geht das Addieren von Brüchen richtig:

5. Fehler: Wie beim Multiplizieren ergibt auch das Dividieren durch Null immer Null

Hier liege häufig ein Trugschluss vor, mahnt Siller an. Gerade weil Null multipliziert mit einer beliebigen Zahl immer auch Null ergebe, hätten viele die Fehlvorstellung, dass 1 durch 0 auch automatisch Null ergebe. Das ist falsch, denn 1 durch 0 ist in der Mathematik nicht definiert. Als Tipp gibt der Professor auch hier mit: Immer daran denken, dass nicht automatisch für die Division die gleichen Regeln gelten, wie für die Multiplikation.

6. Fehler: Wurzeln können auch negative Ergebnisse haben (Bayerischer Wurzelerlass)
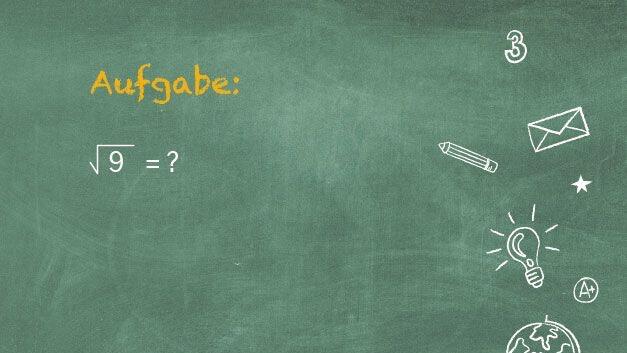
Viele würden denken, dass beispielsweise die Wurzel aus 9 sowohl +3 als auch -3 ist. Die Wurzel einer positiven Zahl ist jedoch immer positiv, erklärt Siller. In der Mathematik nennt man das "rechtseindeutige Relation". Weil die Gegenoperation vom Wurzelziehen aber das Quadrieren ist und auch negative Zahlen quadriert einen positiven Wert ergeben, würden viele annehmen, die Wurzel könne auch negativ sein.
Vielleicht hat sich deshalb der Freistaat Bayern gedacht, er müsse daher für Klarheit sorgen. Denn 1955 hat das bayerische Staatsministerium für Unterricht und Kultus den sogenannten "Bayerischen Wurzelerlass" formuliert. "Der legt per Gesetz fest, dass die Wurzel aus einer positiven Zahl immer positiv ist", so Siller. Für ihn sei das besonders spannend, denn es sei "bundesweit einzigartig, dass so etwas als Erlass einer Dienstbehörde formuliert wird, obwohl es mathematisch doch offensichtlich ist".